# 单调栈
# 面试场上超过窗口最大值概率5倍的结构.
# 单调栈是什么?
一种特别设计的栈结构，为了解决如下的问题：
给定一个可能含有重复值的数组arr，i位置的数一定存在如下两个信息
arr[i]的左侧离i最近并且小于(或者大于)arr[i]的数在哪？
arr[i]的右侧离i最近并且小于(或者大于)arr[i]的数在哪？
如果想得到arr中所有位置的两个信息，怎么能让得到信息的过程尽量快。
如果是暴力方法,那得是O(N^2),但是单调栈可以做到O(N).
# 单调栈结构实现
假设无重复值
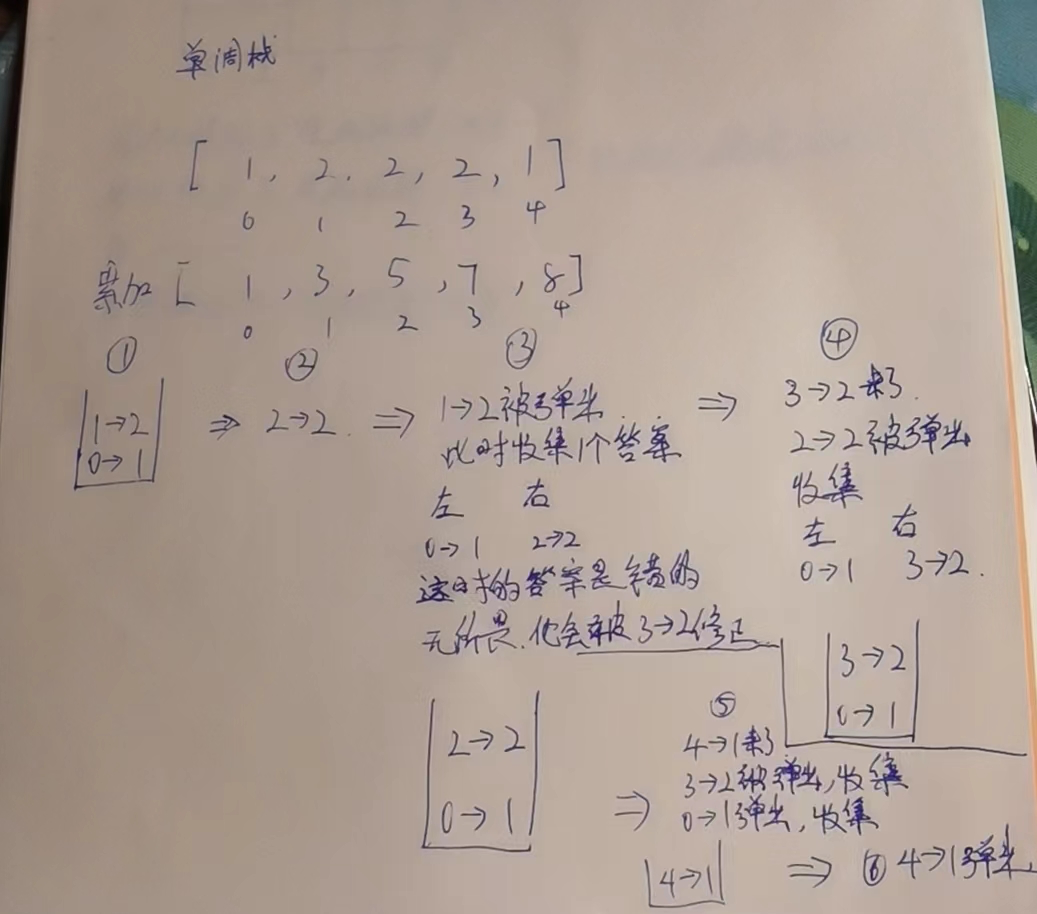
- 准备一个栈.要求,从下往上,是从小到大的,
- 来一个新的数,如果是空的,或者栈顶比他小,那么直接压栈.
- 如果新来的数比栈顶比他大,那么弹出栈顶,此时收集弹出数的答案,让他弹出的,就是他右侧比他小的,他压着的,就是他左边比他小的.
- 遍历完了,如果栈中还有数据,依次弹出,右侧没有被迫让他弹出的,右侧是-1,他压着的就是他左侧离他最近的比他小的,如果没有,也是-1.
// arr = [ 3, 1, 2, 3]
// 0 1 2 3
// [
// 0 : [-1, 1]
// 1 : [-1, -1]
// 2 : [ 1, -1]
// 3 : [ 2, -1]
// ]
public static int[][] getNearLessNoRepeat(int[] arr) {
int[][] res = new int[arr.length][2];
// 只存位置！
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < arr.length; i++) { // 当遍历到i位置的数，arr[i]
//不满足从小到大了,需要弹出,弹出时收集答案
while (!stack.isEmpty() && arr[stack.peek()] > arr[i]) {
int j = stack.pop();
//我压着的就是左边最近的比我小的,没有了就是-1
int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
res[j][0] = leftLessIndex;
//我右边就是逼迫我弹出的
res[j][1] = i;
}
stack.push(i);
}
//遍历完了,栈里还有,依次弹出,弹出时,收集答案.
while (!stack.isEmpty()) {
int j = stack.pop();
int leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
res[j][0] = leftLessIndex;
res[j][1] = -1;
}
return res;
}
假设有重复值
不直接放下标了,组成一个小链表放进去.
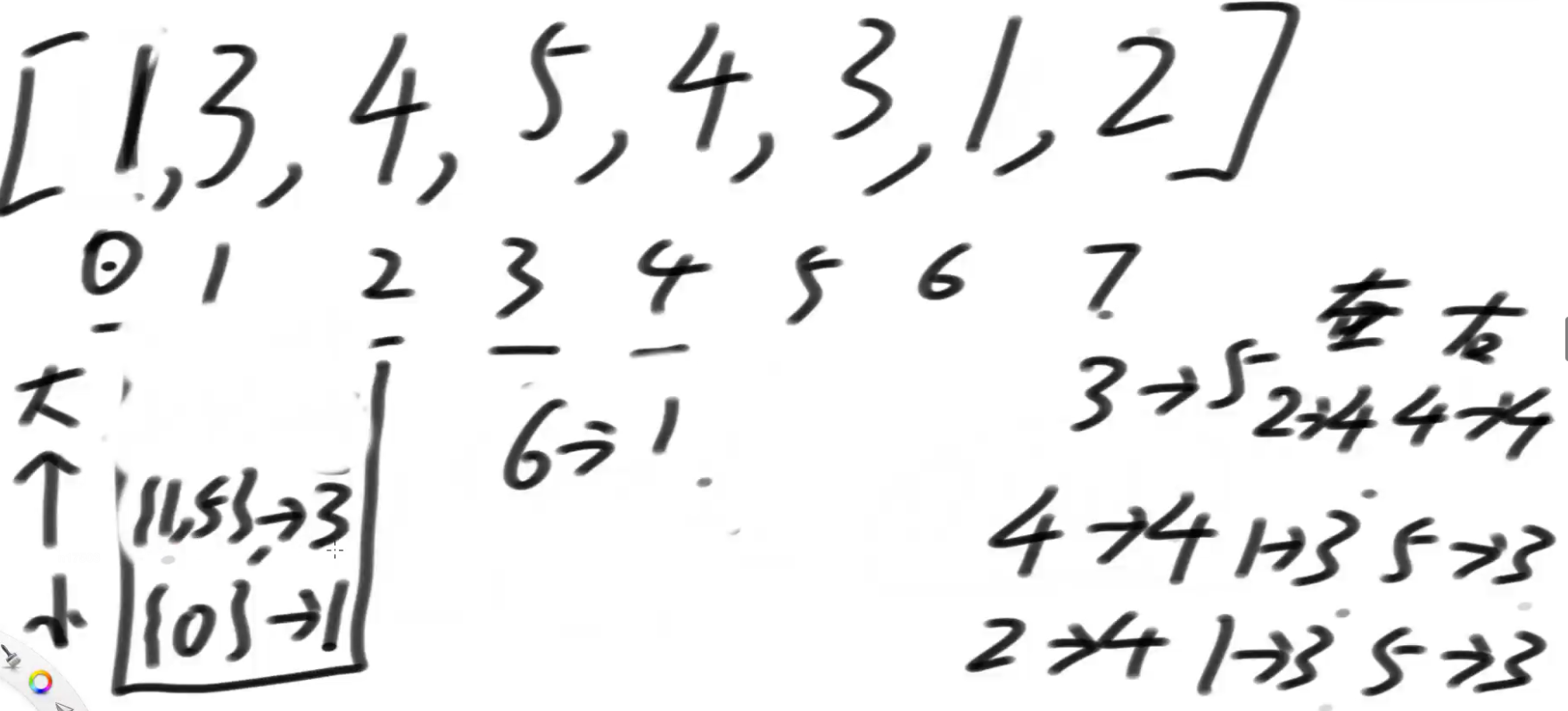
public static int[][] getNearLess(int[] arr) {
int[][] res = new int[arr.length][2];
//有重复值时,栈里放的是个小链表,他们都是同一个值.
Stack<List<Integer>> stack = new Stack<>();
for (int i = 0; i < arr.length; i++) { // i -> arr[i] 进栈
//不满足从小到大了,需要弹出,弹出时收集答案
while (!stack.isEmpty() && arr[stack.peek().get(0)] > arr[i]) {
List<Integer> popIs = stack.pop();
//我弹出时,我压着的链表的最后一个位置,就是离我最近的比我小的
int leftLessIndex = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size() - 1);
for (Integer popi : popIs) {
res[popi][0] = leftLessIndex;
res[popi][1] = i;
}
}
//弹完了,该放了,放的时候注意,如果已经有这个值了,那直接加入链表,否则,创建一个新节点,入栈.
if (!stack.isEmpty() && arr[stack.peek().get(0)] == arr[i]) {
stack.peek().add(Integer.valueOf(i));
} else {
ArrayList<Integer> list = new ArrayList<>();
list.add(i);
stack.push(list);
}
}
//遍历完了,全部弹出.
while (!stack.isEmpty()) {
List<Integer> popIs = stack.pop();
int leftLessIndex = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size() - 1);
for (Integer popi : popIs) {
res[popi][0] = leftLessIndex;
res[popi][1] = -1;
}
}
return res;
}
# 证明
假设无重复值
- 假如栈里,b压着a,此时来了个c,且c<b,根据规则,他会让b弹出.
|b|
|a|
- 右边的证明:c是我遍历到的数,而b,已经在栈里了,所以,b一定在c的左边,那么b~c中间的数,不可能小于b,否则b就不会被c释放掉,而是被中间某个数释放.
- 左边的证明:a,b都在栈里,证明a,在b的左边,那么a~b之间的数,有没有可能<a,不可能,否则,a会被这个数释放掉,有可能a<?<b吗?不可能,因为如果是这样,那么a,b中间一定隔着某个数.因为释放不了.所以,中间的数,一定大于b,这些数都被b释放了.
# 正数子数组累加和 × 这个子数组中最小值 之后的最大值问题
给定一个只包含正数的数组arr，arr中任何一个子数组sub， 一定都可以算出(sub累加和 )* (sub中的最小值)是什么， 那么所有子数组中，这个值最大是多少？
- 核心思路,就是如果最小值固定了,那让累加和尽量的大,就可以得到最大值.
我让每个数都分别当最小值,然后,找到以这个数能扩到的最大的数组范围,算一个乘法值,然后最后比比哪个值更大.返回即可.
这就是一个单调栈,获取一个数,左右两侧比我小的位置以内的最大范围,累加和,✖️自己.
- 做一个前缀和数组,因为我要快速的知道我当前的范围内的累加和是多少.
# 时间复杂度
- 计算前缀和数组.O(N)
- 单调栈,生成每个位置左右位置O(N)
- 针对每个位置,查出累加和O(1),*最小值O(1),算N次,所以O(N).
# 单调栈算法
public static int max2(int[] arr) {
int size = arr.length;
int[] sums = new int[size];
sums[0] = arr[0];
//计算前缀和
for (int i = 1; i < size; i++) {
sums[i] = sums[i - 1] + arr[i];
}
int max = Integer.MIN_VALUE;
//做一个单调栈,栈中元素弹出时候,我就知道他左右比我小的最新的是谁了,那我这时候,算一个最大值.
Stack<Integer> stack = new Stack<Integer>();
for (int i = 0; i < size; i++) {
//>=就弹出,重复值会有算错的,不要紧,会有算对的那个位置
while (!stack.isEmpty() && arr[stack.peek()] >= arr[i]) {
int j = stack.pop();
//i位置数使栈中元素弹出时,i前一个位置肯定就是j位置作为最小值的右侧最大边界了,所以sums[i-1]就是到右侧极限最大范围子数组的累加和,如果栈中有数据,说明从他的左侧往右才是以他为最小值的范围,所以累加和减去栈顶位置的下标的前缀和值.
max = Math.max(max, (stack.isEmpty() ? sums[i - 1] : (sums[i - 1] - sums[stack.peek()])) * arr[j]);
}
stack.push(i);
}
while (!stack.isEmpty()) {
int j = stack.pop();
max = Math.max(max, (stack.isEmpty() ? sums[size - 1] : (sums[size - 1] - sums[stack.peek()])) * arr[j]);
}
return max;
}
# 直方图最大面积问题
给定一个非负数组arr，代表直方图 返回直方图的最大长方形面积
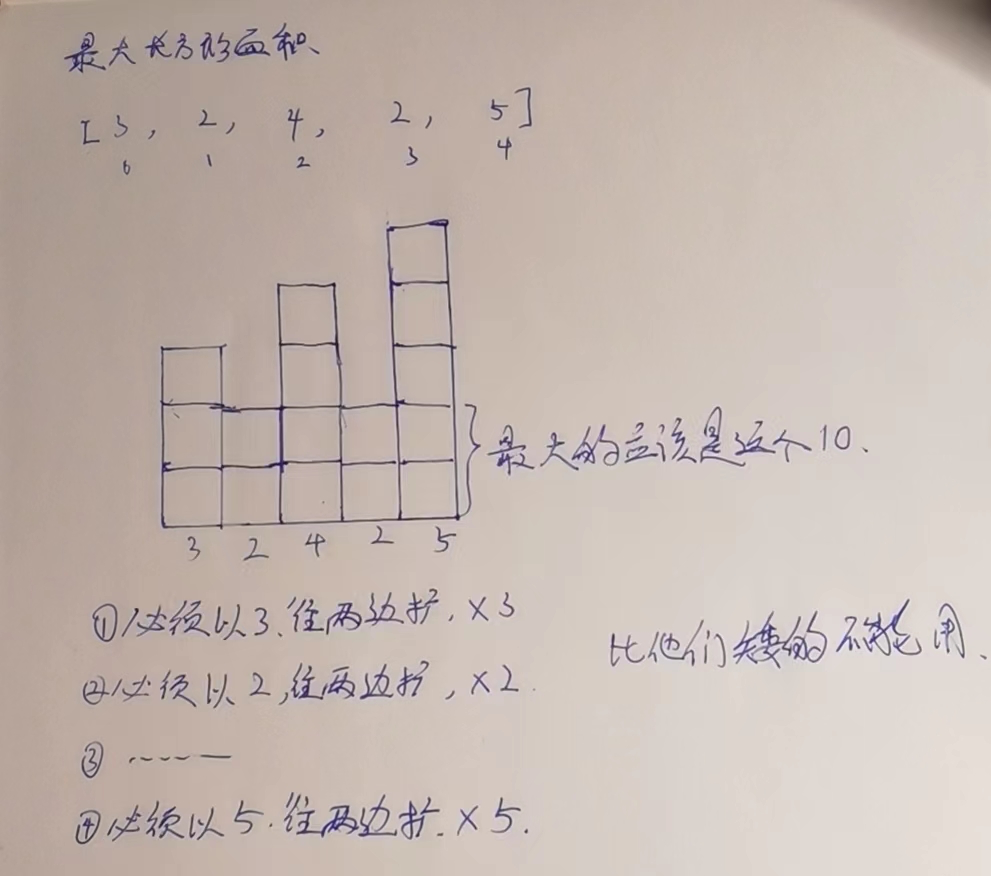这个题解题思路,就是每个格子的高度做高,左右能扩到最大的宽度*自己的高度,跟上面那个题没什么区别.
public static int largestRectangleArea1(int[] height) {
if (height == null || height.length == 0) {
return 0;
}
int maxArea = 0;
Stack<Integer> stack = new Stack<Integer>();
for (int i = 0; i < height.length; i++) {
while (!stack.isEmpty() && height[i] <= height[stack.peek()]) {
int j = stack.pop();
int k = stack.isEmpty() ? -1 : stack.peek();
int curArea = (i - k - 1) * height[j];
maxArea = Math.max(maxArea, curArea);
}
stack.push(i);
}
while (!stack.isEmpty()) {
int j = stack.pop();
int k = stack.isEmpty() ? -1 : stack.peek();
int curArea = (height.length - k - 1) * height[j];
maxArea = Math.max(maxArea, curArea);
}
return maxArea;
}
# 全部由1组成的最大子矩阵问题
这是个力扣原题 https://leetcode.com/problems/maximal-rectangle/ 难倒众多学员的一个德高望众的题.
给定一个二维数组matrix，其中的值不是0就是1， 返回全部由1组成的最大子矩形，内部有多少个1
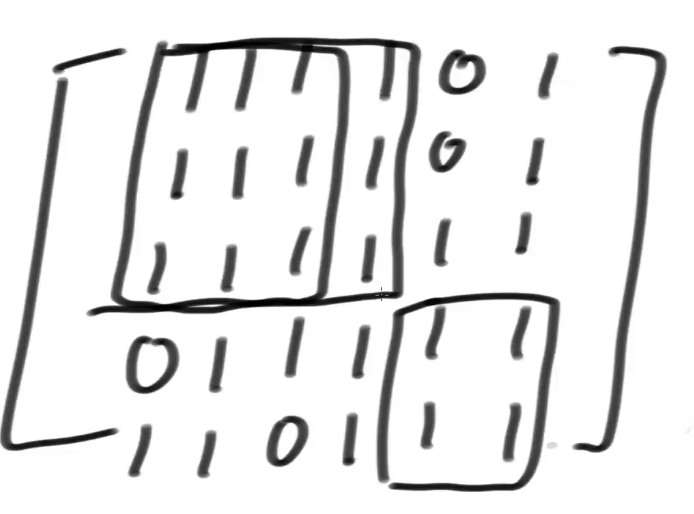
# N*N的大矩阵,有多少子矩阵(复杂度)?
N^4个.随便点一个点是N^2,再随便点一个点,是N^2,所以他俩组成的矩阵,是N^4.
暴力解:我先列举出有多少个子矩阵,已经是N^4,再验证这个每个子矩阵是不是都1,再来N^2,综合.O(N^6)
# 优雅的解 压缩数组+ 单调栈
public static int maximalRectangle(char[][] map) {
if (map == null || map.length == 0 || map[0].length == 0) {
return 0;
}
int maxArea = 0;
int[] height = new int[map[0].length];
for (int i = 0; i < map.length; i++) {
for (int j = 0; j < map[0].length; j++) {
//如果当前行的有0,那就重置,否则+1
height[j] = map[i][j] == '0' ? 0 : height[j] + 1;
}
//一行行下去找最大值
maxArea = Math.max(maxRecFromBottom(height), maxArea);
}
return maxArea;
}
// height是正方图数组
public static int maxRecFromBottom(int[] height) {
if (height == null || height.length == 0) {
return 0;
}
int maxArea = 0;
Stack<Integer> stack = new Stack<Integer>();
for (int i = 0; i < height.length; i++) {
while (!stack.isEmpty() && height[i] <= height[stack.peek()]) {
int j = stack.pop();
int k = stack.isEmpty() ? -1 : stack.peek();
int curArea = (i - k - 1) * height[j];
maxArea = Math.max(maxArea, curArea);
}
stack.push(i);
}
while (!stack.isEmpty()) {
int j = stack.pop();
int k = stack.isEmpty() ? -1 : stack.peek();
int curArea = (height.length - k - 1) * height[j];
maxArea = Math.max(maxArea, curArea);
}
return maxArea;
}
# 返回全部由1组成的子矩形数量
给定一个二维数组matrix，其中的值不是0就是1，返回全部由1组成的子矩形数量
假设到总矩阵某一层,压缩数组是[5,1,4,2,2,1]时
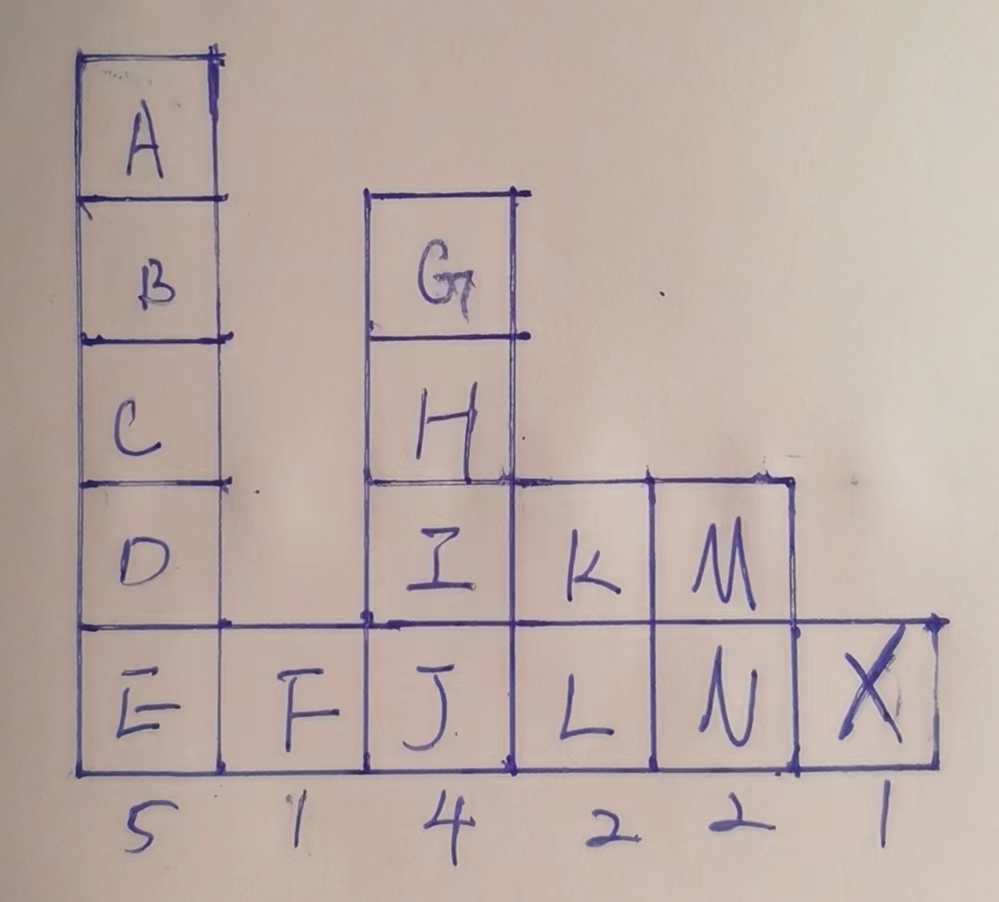
0→5先压栈,
1→1来了,他迫使5出栈,因为让他出来的1不等于5,此时计算5~2层的,左右不可达范围内所有结果,此时就是ABCD区域.
1→1压栈,2→4来了,他比1大,所以直接进栈.
3→2来了,他迫使2→4出栈,因为让他出来的4不等于2,此时计算4~3层的,左右不可达范围内所有结果,此时就是GH区域.
4→2来了,他迫使3→2出栈,但是此时出来的2等于自己的2,此时不计算,等着后来这个2出来时候统一计算,
5→1来了,他迫使4→2出栈,此时2!=1,计算4→2的,2~2层,左右不可达位置所有结果,此时就是IKM区域.
后面没有了,栈中还有数,弹出,此时5→1出栈,左边不可达-1,右边也没有比我小的,计算1~1层,左右不可达位置所有结果,此时就是EFJLNX区域.
至此,所有格子都收集过了.'
特别声明格子的计算方法:以0列为例子,他只有1列.根据公式(X-max(Y,Z)) * ((L * (L+1))/2)
公式计算方式
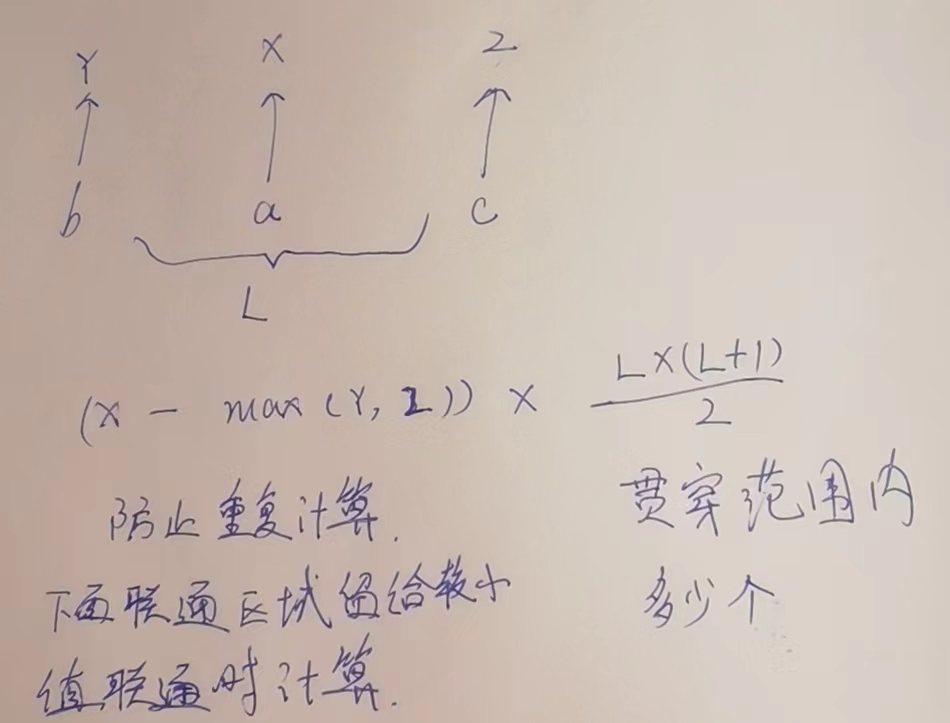
当遍历到第一行的时候,收集的就是A (1-0) * 1个
当遍历到第二行的时候,收集的就是B,AB (2-0) * 1个
当遍历到第三行的时候,收集的就是C,BC,ABC (3-0) * 1个
当遍历到第四行的时候,收集的就是D,CD,BCD,ABCD (4-0)*1个
当遍历到第五行的时候,收集的就是DE,CDE,BCDE,ABCDE,(5-1)*1个
为什么第五行,要减一,因为最底下的格子等着X位置联通成整个区域的时候才计算呢.
public static int numSubmat(int[][] mat) {
if (mat == null || mat.length == 0 || mat[0].length == 0) {
return 0;
}
int nums = 0;
int[] height = new int[mat[0].length];
for (int i = 0; i < mat.length; i++) {
for (int j = 0; j < mat[0].length; j++) {
height[j] = mat[i][j] == 0 ? 0 : height[j] + 1;
}
nums += countFromBottom(height);
}
return nums;
}
// 比如
// 1
// 1
// 1 1
// 1 1 1
// 1 1 1
// 1 1 1
//
// 2 .... 6 .... 9
// 如上图，假设在6位置，1的高度为6
// 在6位置的左边，离6位置最近、且小于高度6的位置是2，2位置的高度是3
// 在6位置的右边，离6位置最近、且小于高度6的位置是9，9位置的高度是4
// 此时我们求什么？
// 1) 求在3~8范围上，必须以高度6作为高的矩形，有几个？
// 2) 求在3~8范围上，必须以高度5作为高的矩形，有几个？
// 也就是说，<=4的高度，一律不求
// 那么，1) 求必须以位置6的高度6作为高的矩形，有几个？
// 3..3 3..4 3..5 3..6 3..7 3..8
// 4..4 4..5 4..6 4..7 4..8
// 5..5 5..6 5..7 5..8
// 6..6 6..7 6..8
// 7..7 7..8
// 8..8
// 这么多！= 21 = (9 - 2 - 1) * (9 - 2) / 2
// 这就是任何一个数字从栈里弹出的时候，计算矩形数量的方式
public static int countFromBottom(int[] height) {
if (height == null || height.length == 0) {
return 0;
}
int nums = 0;
//原装的栈效率比较低,这里用数组替换.
int[] stack = new int[height.length];
int si = -1;
for (int i = 0; i < height.length; i++) {
while (si != -1 && height[stack[si]] >= height[i]) {
int cur = stack[si--];
if (height[cur] > height[i]) {
int left = si == -1 ? -1 : stack[si];
int n = i - left - 1;
int down = Math.max(left == -1 ? 0 : height[left], height[i]);
nums += (height[cur] - down) * num(n);
}
}
stack[++si] = i;
}
while (si != -1) {
int cur = stack[si--];
int left = si == -1 ? -1 : stack[si];
int n = height.length - left - 1;
int down = left == -1 ? 0 : height[left];
nums += (height[cur] - down) * num(n);
}
return nums;
}
public static int num(int n) {
return ((n * (1 + n)) >> 1);
}
← 滑动窗口内最大值或最小值问题 KMP算法 →