冯手力-java学习之路

# KMP算法

# 每年必考高频题

# KMP算法的定义

假设字符串str长度为N，字符串match长度为M，M <= N
想确定str中是否有某个子串是等于match的。
时间复杂度O(N)

java的indexOf.

# KMP是三个人名缩写.

# KMP算法核心

  1. 如何理解next数组

  2. 如何利用next数组加速匹配过程，优化时的两个实质！

# 暴力方法时间复杂度

每当第一个匹配到的时候,后面挨个遍历匹配,所以是M*N次 复杂度O(N*M),

# 算法核心1-next数组-i位置以前的最大前缀=最大后缀的长度

match串,每个字符,都对应一个next数组的值.

首先有2个重要规定

  1. 任何字符串,任何,都是next[0]=-1,next[1]=0.
  2. 前后缀匹配不到最大长度,

其次,对于任何i位置来说,他对应的next[i] = 最大前缀串与最大后缀串相等的长度,例子如图

注意啊,i位置的信息,是和他本身没有任何关系的,是求他前面的.

例如:abcabck,假设,求k位置,和k的字符的位置是没有任何关系的,是他之前的字符串的能匹配上的最长前缀和最长后缀.

,next[6] = 3,next[0] = -1, next[1] = 0

image-20240619193746657

# 利用next数组加速过程

暴力算法的最吃亏的地方就是,M-2位置的都对上了,只有M-1不对,但是再次匹配到M[0]时候,又得全部再配一遍,对已经配过的,没有提示作用.那么KMP算法是怎么加速的呢.

  1. 我们先对s2字符串求了next数组(谁被match,谁求next数组.)
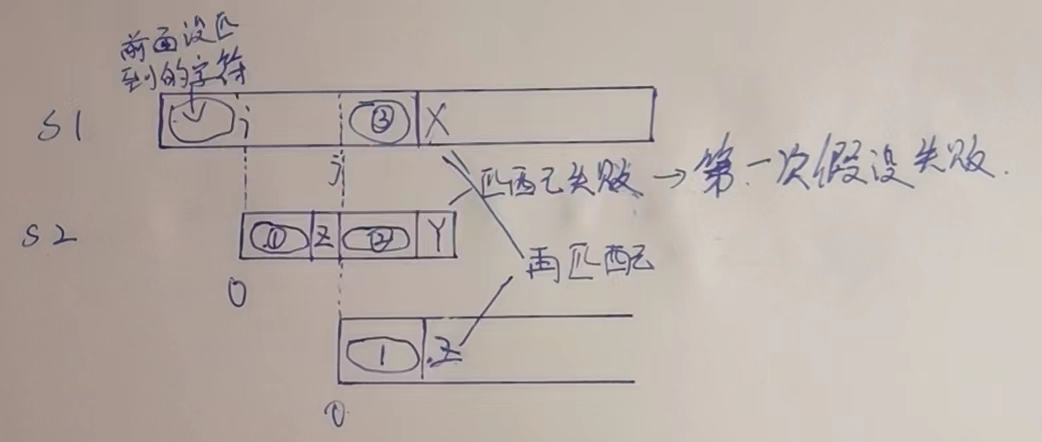
  2. 假设在s1[i]== s2[0]了,那我们继续匹配,直到s1某个字符!=s2某个字符了.例如图中,s1[X]!=s2[Y]
  3. 此时我们可以知道next[Y]的值是多少,因为next数组的计算规则,Y前面前后缀相等最大的一段,就是①==②的,因为我们是从i一直推到X,才对不上的,所以③一定是== ②的.所以①==③,也就是j~X-1范围,就是②范围
  4. 如果我们确定i~j位置,绝对是没有用的区域,绝对配不出来(后面证明),是不是我们也知道①==③,所以我们直接让j位置和0对齐,从X是否==Z开始判断即可,看到了吗,这里加速了,.
  5. 如果s1[X]==s2[Z],那么继续都下一个继续比,如果不等,Z也有自己的最大前后缀相等数组,0位置推到j'位置,继续重复上面的步骤.
  6. 如果一直推推推,s1[X]连s2[0]位置都没配上,那s1换下一个开头吧,换s1[X+1]匹配s2[0],什么时候匹配到了,继续上面的步骤.

image-20240619195020246

# 证明i~j之间任何一个k位置出发,都绝对配不出s2来.

这是上面步骤4的证明.当X,Y位置不相等时候,i~j位置中任何k位置出发,绝对配不出来.i~j位置是无效区域.不需要验证.

我们反证,假设k位置出发,可以配出来s2.

s1 k k+1 k+2 .. ?

s2 0 1 2, ...M

就是说上面的都能配出来.

我先画个图

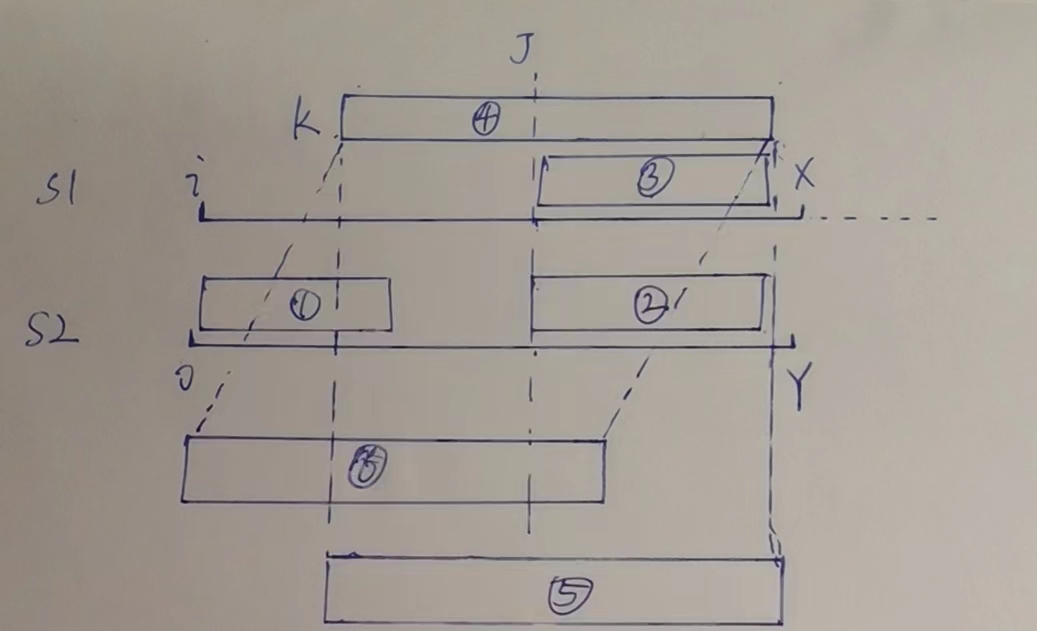
image-20240619224435225

好,你号称k出发到X可能能配出来s2,好那你起码k~X得能配出⑥(等量前缀)这段吧,

继续,别忘了一个结论,那就是,s1[i]对应s2[0],一直到s1[X],s2[Y]才折了,那到Y-1前,你肯定一路都相等吧,也就是说④==⑤吧,如果你④==⑤,可是我④==⑥,

不对劲,k在j左边,④一定比③大,?那就是说Y之前存在一个更长的前缀⑥和后缀⑤能匹配上,那就和next数组求的冲突了,我next数组不可能求错,那只能是假设错了.

# KMP的code

x,y指的是画圈的位置,

public static int getIndexOf(String s1, String s2) {
		if (s1 == null || s2 == null || s2.length() < 1 || s1.length() < s2.length()) {
			return -1;
		}
		char[] str1 = s1.toCharArray();
		char[] str2 = s2.toCharArray();
		int x = 0;
		int y = 0;
		// O(M) m <= n
		int[] next = getNextArray(str2);
		// O(N)
		while (x < str1.length && y < str2.length) {
			//从头开始,如果匹配上了,那就两个串下一个字符接着比.
			if (str1[x] == str2[y]) {
				x++;
				y++;
				//否则到某个断了,如果跟我第二串第1个字符都比不上,那换个直接串1下一个重新试试吧
			} else if (next[y] == -1) { // y == 0
				x++;
				//否则不一定一个都对不上呢,那就是跳到next数组值上,相当于整个串2往后推.
			} else {
				y = next[y];
			}
		}
		//只有x或者y越界了,才会跳出,如果是y越界,只可能是s2全部匹配到了,那就是从x位置-y位置,就是字符串出现位置,否则x越界,没找到.
		return y == str2.length ? x - y : -1;
	}

# 估算复杂度

三个分支分别估算.

X最大是N,Y最大是M(到不了N)

X(max:N) X-Y(max:M) 结果
分支1 ↑ ↑ 不变
分支2 ↑ 不变 升高
分支3 不变 ↓ 升高

x-y什么含义,就是数学上的求差,单独的X和单独的Y,变化是不是看不出来啊

结论 最大,2N,收敛于N

# next数组加载过程

i-1位置的数,要对i位置有个提示作用.(前一个位置的数要对后一个数有提示作用)

规定:0位置是-1,1位置是0,2位置看0==1位置,等就是1否则就是0.

再往上.

看i-1位置是否等于前缀下一个,如果相等,就是i-1位置+1

注意:i位置一定不可能比i-1位置大超过1.

验证.

如果19位置是7,代表0-6位置==12-18位置,最长前缀后缀都是7嘛.

如果20位置是9,代表0-8==11-19,最长前缀后缀都是9嘛.那么19位置往前看,就应该是0-7==11-18,应该是8而不应该是7.

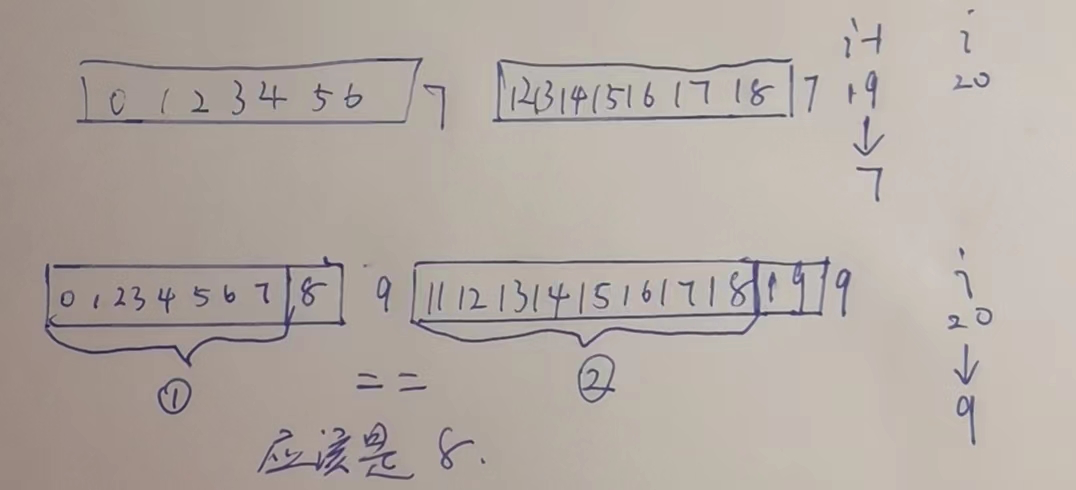
image-20240619235354295

所以,next数组的值最大是i-1位置+1

如果i-1不等于前缀+1个字符,那么,找到前缀+1位置的next的值,看看这个值的下一个是否等于i-1位置的字符.如图所示

image-20240619235636268

public static int[] getNextArray(char[] str2) {
   if (str2.length == 1) {
      return new int[] { -1 };
   }
   int[] next = new int[str2.length];
   next[0] = -1;
   next[1] = 0;
   int i = 2; // 目前在哪个位置上求next数组的值
   int cn = 0; // 当前是哪个位置的值再和i-1位置的字符比较,较大的长度的匹配不上,咋弄呢,缩呗.看看他前面的最长到哪.
   while (i < next.length) {
      if (str2[i - 1] == str2[cn]) { // 配成功的时候 2.按上面图的例子扩到7,配上了,7位置是1.  3.下个位置又相等,8位置是2.下个位置又相等9位置是cn -> 3.
         next[i++] = ++cn;
      } else if (cn > 0) {//4,按上图例子,扩到10位置,配不上了,跳到next数组cn的位置
         cn = next[cn];
      } else {//1. 按上面图的例子扩到6都是0
         next[i++] = 0;
      }
   }
   return next;
}

# 练习题一

我们说有一个字符串,例如123456,234561,或者345612.......是旋转串.

问str1,str2是否互为旋转串.

这个题很经典,也很骚.就是个kmp题,首先比较长度,不一样长,直接排,然后两个str1拼成一个大的串,然后我们就看,str2在这个结果上出现没有.

# 练习题二

两棵树,A树比B树大,请问B树是不是A树的子树,

子树就是全都得要,不能抛下某个分支.

这个题就是将2颗树都序列化,然后利用kmp,如果b树字符串出现在a树中了,那B就是A的子树.

← Manacher算法 →